About us

This website is part of the initiative of the UC Berkeley Physics Department to introduce computational techniques into the undergraduate physics curriculum. This website assists instructors in browsing pre-existing problems, and creating and assigning problem sets to their students.

Technical background

Here is a set of tutorials to learn the computational materials required for these problems.

The Jupyter notebook, a generalization of the Mathematica notebook, has emerged as the preferred medium to share and annotate code in the data analysis community (and in some of the physical computing communities), and Python has similarly emerged as the preferred programming language. Thus these are natural choices for instructional material.

Using Python-based Jupyter notebooks has the additional advantage that all members of the Berkeley community can access the DataHub, which is a JupyterHub server hosted in the cloud that allows users to run Jupyter notebooks. Not only does this lower the barrier of entry (anybody with access to a browser can use these resources) but it also standardizes the computing environment used by the students (students don’t have to install anything on their local machines and GSIs don’t need to debug the myriad problems caused by differing environments).

Computational problems are stored in a private GitHub repository owned by the Berkeley Physics organization. This website interfaces the problem bank, enabling the problems to be browsed, searched, and viewed without requiring familiarity with any of the tools described above, and automates the process of formatting, compiling, and sharing problem sets with students.

Why introduce computation in physics?

This is a response not only to student demand (over half the respondents to a major exit survey indicated the integration of computational tools to be their most desired change in the undergraduate physics curriculum), but also to trends in the community and beyond. A student familiar with numerical computation is more useful in several academic and industrial contexts, improving their future prospects. Several PIs and researchers can attest to the influence of this practical skill set in hiring decisions. Computing has revolutionized research, business, and daily life and it is about time that this is reflected in physics education.

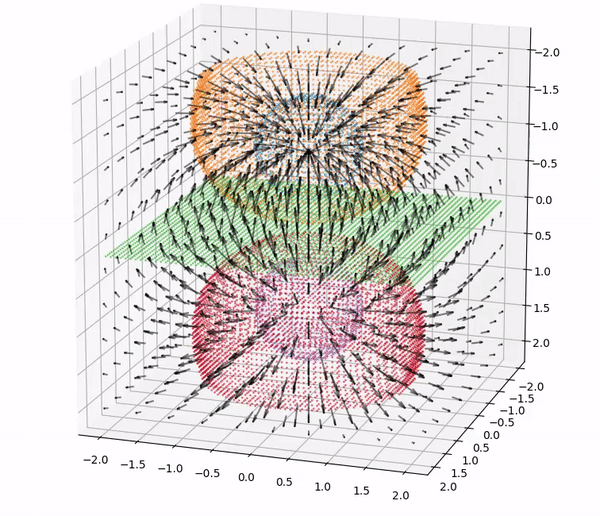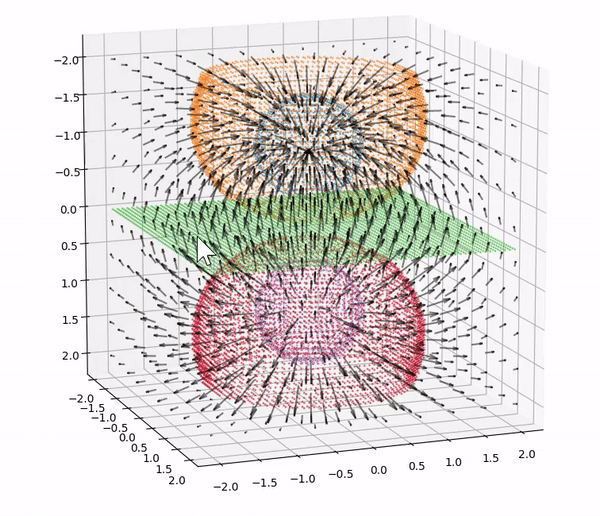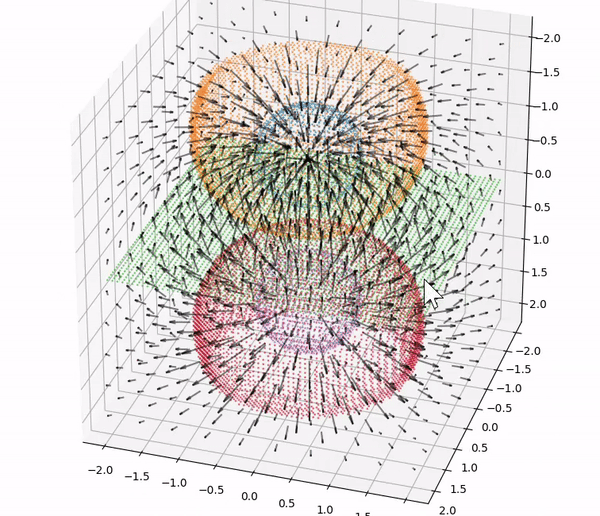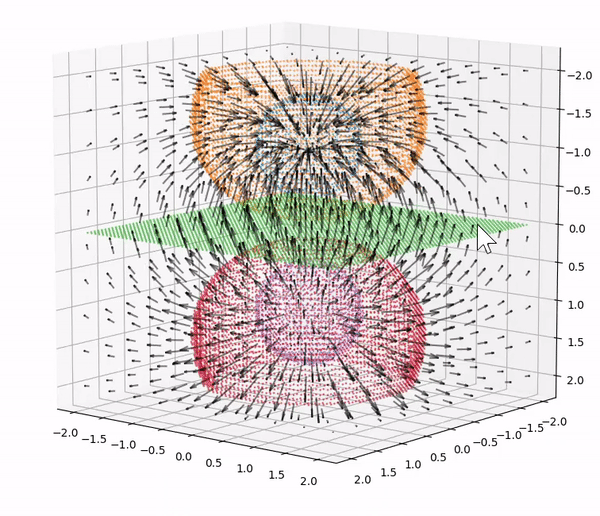
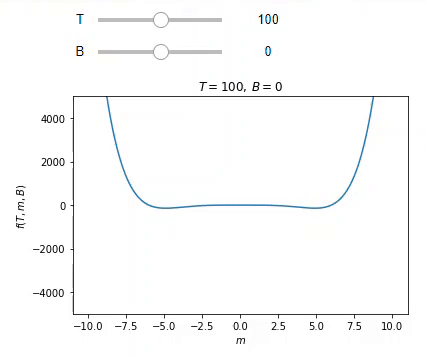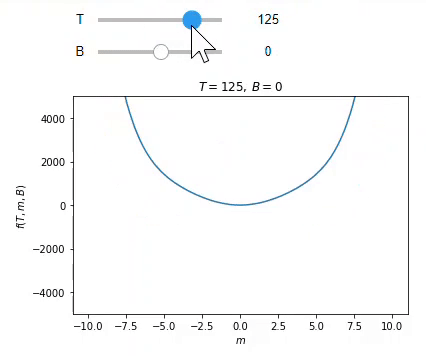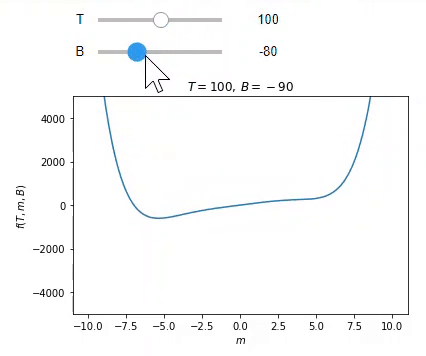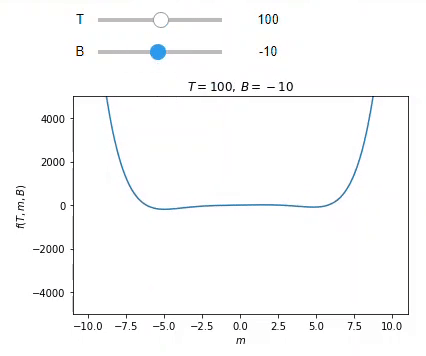
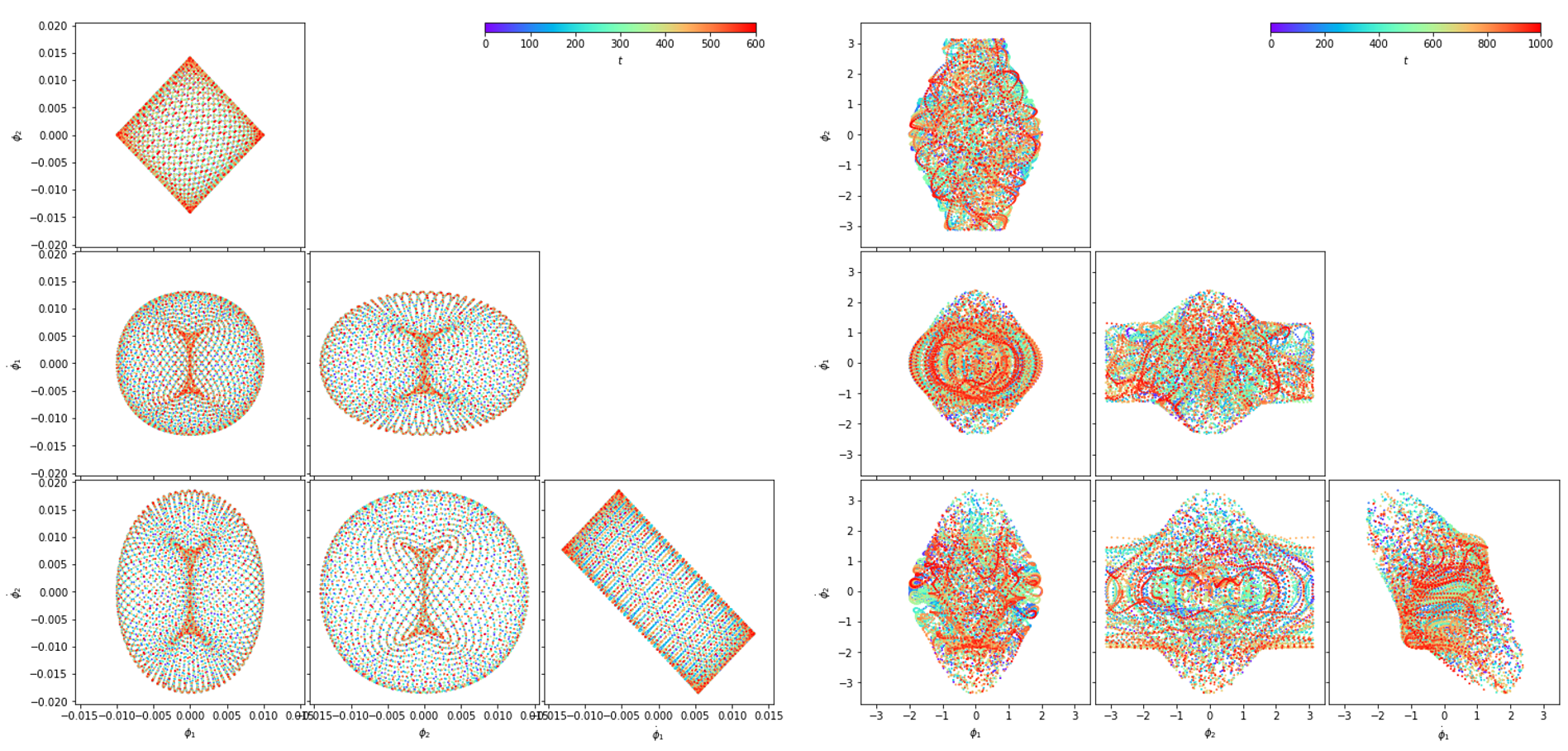
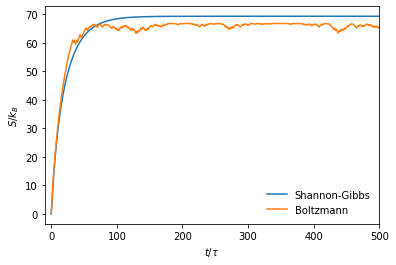
One of the tools enabled by computing is the ability to create and interact with visualizations of physical objects, principles and phenomena. While the ability to create effective plots to present relationships is an important skill in scientific communication that should be taught in its own right, providing students with visualizations to interact with can also help them in understanding concepts ranging from vectors and waves to Landau theory without requiring familiarity with computation. Students often struggle with the 3D visualization of vector fields, which can be taught effectively with computational aid.

Computational tools allow us to solve equations that are impossible or extremely tedious to solve analytically using elementary functions. Even in some cases that are solvable analytically, computers allow us to scale systems up beyond the point where students can reasonably be expected to study them analytically, increasing the range of physics accessible to the student. “Simulating” systems provides even theorists the ability to perform “experiments” to test their hypotheses, refine their intuition, and guide them in determining which statements can be proven analytically. Increasing the complexity of the systems we like to analyze could eventually assist in the reduction of simplicity bias in physics.

Information theory connects statistical mechanics to computer science. Techniques like simulated annealing utilize physical principles to solve unrelated problems. The link between physical and computational complexity is made apparent by, e.g., tensor networks. The application of physical concepts to non-physics problems is something our current curriculum does not address. Making our students computer-literate would, at the least, encourage them to explore these interfaces with practical application, and help ground theoretical understanding.

Examples

Interactive visualisations can help students understand concepts without requiring any computer knowledge. The animation are from exercises that teach students about, from left to right and then top to bottom: 2d vectors, electric dipoles, 3d rigid rotation, and Landau theory.

Computational tools allow students to study systems that are beyond the scope of analytical tools. In this exercise, students compare the double pendulum in the small-angle and nonlinear regimes.

Computational tools allow students to simulate systems, performing "experiments" rapidly and conveniently, and analyse the results of real and simulated experiments to obtain physical conclusions. This exercise compares the entropy of a single outcome of the system described by the Ehrenfest model, conditioned on all the particles/fleas being in one container/dog at $t=0$, with and without knowledge of the macrostate at subsequent times, which reinforces to students the statistical and emergent nature of the second law of thermodynamics.